Fractional Part Function

Here you will learn definition, graph, domain and range of fractional part function.

Let’s begin –

Definition : For any real number x, we use the symbol {x} to denote fractional part or decimal part of x.

For example, {3.45} = 0.45, {-2.75} = 0.25, {-0.55} = 0.45, {3} = 0, {-7} = 0 etc.

The function f : R $\rightarrow$ R defined by f(x) = {x} for all x $\in$ r is called the fractional part function.

It is evident from the definition that

f(x) = {x} = x – [x] for all x $\in$ R

Also Read : Types of Functions in Maths – Domain and Range

Graph of Fractional Part Function

The graph of the fractional part function is as shown below.

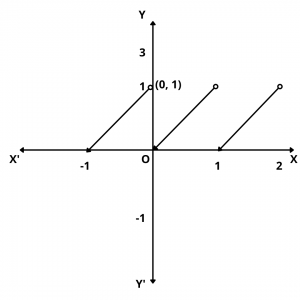
$fractional part function$

We observe that the domain is the set of R of all real numbers and the range is the set [0, 1).

Domain : R

Range : [0, 1)