How to Calculate Slope of Line
If given line makes an angle \(\theta\) (0 \(\le\) \(\theta\) \(\le\) 180 , \(\theta\) \(\ne\) 90) with positive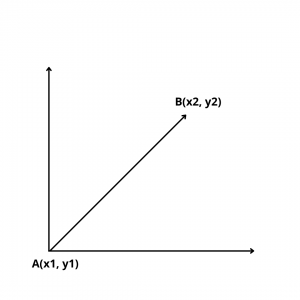
direction of x-axis, then slope of line will be tan\(\theta\) and is usually denoted by letter m.
i.e. m = tan\(\theta\).
Slope of line Passing Through Two Points Formula
If A(\(x_1,y_1\)) and B(\(x_2,y_2\)) are the two points on a straight line & \(x_1\) \(\ne\) \(x_2\) then the formula for slope of line passing through two points is
m = \(y_2-y_1\over {x_2-x_1}\).
By using above formula, we can easily calculate the slope of line between two points.
Example : Find the slope of a line between the points A = (2, 0) and B = (4,6).
Solution : Here \(x_1, y_1\) = (2, 0) and \(x_2, y_2\) = (4, 6).
By using slope of line formula,
m = \(y_2-y_1\over {x_2-x_1}\) = \(6-0\over 4-2\)
m = \(6\over 2\)
\(\implies\) m = 3.
Hence slope of line is 3.
Slope of Vertical Lines – Slope of Line Parallel to y-axis :
A vertical line is a line, parallel to y-axis and goes straight, up and down, in a coordinate plane.
In this case, \(\theta\) = 90
m = tan\(\theta\) = tan 90 = \(\infty\)
i.e. m does not exist when the slope of line is parallel to y-axis.
Slope of Horizontal Lines – Slope of Line Parallel to x-axis :
A horizontal line which is parallel to x-axis and goes straight, left and right in the coordinate plane.
In this case, \(\theta\) = 0
m = tan\(\theta\) = tan 0 = 0
i.e. m = 0
Slope of Parallel Lines :
Let \(m_1\) and \(m_2\) be slopes of two given lines,
then, \(m_1\) = \(m_2\)
Slope of Perpendicular Lines :
Let \(m_1\) and \(m_2\) be slopes of two given lines,
then, \(m_1\) \(\times\) \(m_2\) = -1
Slope of Line Equation :
The slope of line equation is also called equation of line in slope form and is written as
y = mx + c.
where m is the slope of line and c is the intercept on y-axis.
Example : Find the slope of a line whose equation is y = 3x + 4.
Solution : Given equation is y = 3x + 4
Comparing it with slope of line equation, y = mx + c
we get, m = 3.
Hope you learnt how to calculate slope of line, learn more concepts of straight lines and practice more questions to get ahead in the competition. Good luck!