Here you will learn what is hyperbola, equation of the hyperbola and graph of a hyperbola with basic definitions like vertex, foci and directrix.
Let’s begin –
What is Hyperbola ?
A hyperbola is the locus of a point in a plane which moves in a plane in such way that the ratio of its distance from fixed point called focus in the same plane to its distance from a fixed line called Directrix is always constant and which is always greater than unity.
The constant ratio is generally denoted by e and is known as the eccentricity of hyperbola.
If S is the focus, ZZ’ is the directrix and P is any point on the hyperbola, then by the definition
\(SP\over PM\) = e \(\implies\) SP = ePM
Equation of the Hyperbola
The equation of the hyperbola is
\(x^2\over a^2\) – \(y^2\over b^2\) = 1,
where \(b^2\) = \(a^2(e^2 – 1)\) or \(a^2\) + \(b^2\) = \(a^2e^2\) i.e. \(e^2\) = \(1 + {b^2\over a^2}\)
= 1 + \(({conjugate axis\over transverse axis})^2\)
Example : Find the equation of the hyperbola whose directrix is 2x + y = 1, focus (1, 2) and eccentricity \(\sqrt{3}\).
Solution : Let P(x, y) be the any point on the hyperbola and PM is perpendicular from P on the directrix,
Then by definition SP = ePM
\((SP)^2\) = \(e^2(PM)^2\) \(\implies\) \((x-1)^2 + (y-2)^2\) = 3\([{2x + y – 1\over {\sqrt{4 + 1}}}]^2\)
5\((x^2 + y^2 – 2x – 4y + 5)\) = 3\((4x^2 + y^2 + 1 + 4xy – 2y – 4x)\)
\(7x^2 – 2y^2 + 12xy – 2x + 14y – 22\) = 0
which is required equation of the hyperbola.
Graph of a Hyperbola & Definitions :
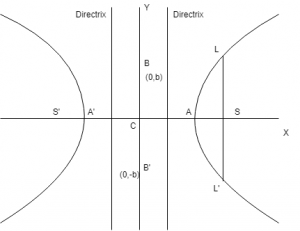
(a) Foci : S = (ae, 0) and S’ = (-ae, 0)
(b) Equation of directrices of hyperbola : x = \(a\over e\) and x = \(-a\over e\)
(c) Vertices : A = (a, 0) and A’ = (-a, 0)
(d) Latus Rectum of hyperbola : The line passes through focus is called latus rectum of hyperbola.
Length = \(2b^2\over a\) = \({(conjugate axis)}^2\over {transverse axis}\) = 2a(\(e^2\) – 1) = 2e (distance from focus to directrix)
Equation : x = \(\pm\)ae
Ends : L(ae, \(b^2\over a\)), L'(ae, -\(b^2\over a\)), L1(-ae, \(b^2\over a\)), L1′(-ae, -\(b^2\over a\))
(e) Transverse axis of hyperbola : The line segment A’A of length 2a in which the foci S’ & S both lie is called the transverse axis of the hyperbola.
(f) Conjugate axis of hyperbola : The line segment B’B between two points B’ = (0, -b) & B = (0, b) is called the conjugate axis of the hyperbola.
Example : Find the coordinates of foci, the eccentricity and equations of directrix for the hyperbola \(9x^2-16y^2-72x+96y-144\) = 0
Solution : Equation can be rewritten as \({(x-4)}^2\over 4^2\) – \({(y-3)}^2\over 3^2\) = 1 so a = 4, b = 3.
\(b^2\) = \(a^2(e^2 – 1)\) given e = \(5\over 4\)
Foci : X = \(\pm\)ae, Y = 0 gives the foci as (9, 3), (-1, 3)
Centre : X = 0, Y = 0 i.e. (4, 3)
Directrices : X = \(\pm\)\(a\over e\) i.e. x – 4 = \(\pm\)\(16\over 5\)
\(\therefore\) directrices are 5x – 36 = 0; 5x – 4 = 0.
Hope you learnt what is hyperbola and how to find equation of the hyperbola, learn more concepts of hyperbola and practice more questions to get ahead in the competition. Good luck!