Solution :
The general solution of \(cot \theta\) = 0 is given by \(\theta\) = \((2n + 1){\pi\over 2}\), n \(\in\) Z.
Proof :
We have,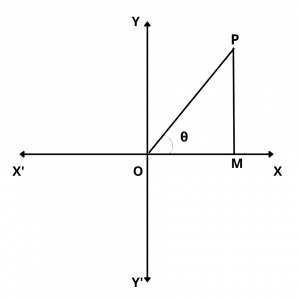
\(cot \theta\) = \(OM\over PM\)
\(\therefore\) \(cot \theta\) = 0
\(\implies\) \(OM\over PM\) = 0
\(\implies\) OM = 0
\(\implies\) OP coincides with OY or OY’
\(\implies\) \(\theta\) = \(\pm{\pi\over 2}\), \(\pm{3\pi\over 2}\), \(\pm{5\pi\over 2}\), …….
\(\implies\) \(\theta\) = \((2n + 1){\pi\over 2}\), n \(\in\) Z
Hence, \(\theta\) = \((2n + 1){\pi\over 2}\), n \(\in\) Z is the general solution of \(cot \theta\) = 0.