Here you will learn what is exponential function graph, formula, domain and range.
Let’s begin –
Exponential Function Formula
Definition : If a is a positive real number other than unity, then a function that associates each x \(\in\) R to \(a^x\) is called the exponential function.
In other words, a function f : R \(\rightarrow\) R defined by f(x) = \(a^x\), where a > 0 and a \(\ne\) 1 is called the exponential function.
Formula : It is defined by the formula f(x) = \(a^x\).
where a > 0 and a \(\ne\) 1
a is a constant, which is the base of the function
x is any variable.
Also Read : Types of Functions in Maths – Domain and Range
Exponential Function Graph
Case 1 : When a > 1,
We observe that the values of y = f(x) = \(a^x\) increase as the value of x increase.
Also, f(x) = \(\begin{cases} < 1, & \text{for}\ x > 0 \\ = 1, & \text{for}\ x = 0 \\ > 1, & \text{for}\ x < 0 \end{cases}\).
Thus, the graph f(x) = \(a^x\) for a > 1 is :
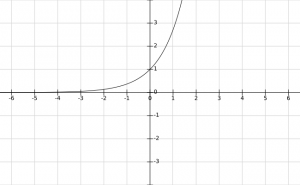
Case 2 : When 0 < a < 1
In this case, the values of y = f(x) = \(a^x\) decrease with increase in x and y > 0 for all x \(\in\) R.
Also, f(x) = \(\begin{cases} > 1, & \text{for}\ x > 0 \\ = 1, & \text{for}\ x = 0 \\ < 1, & \text{for}\ x < 0 \end{cases}\).
Thus, the graph f(x) = \(a^x\) for 0 < a < 1 is :
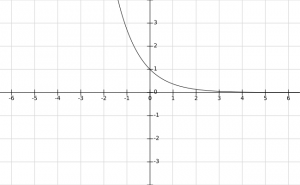
Domain and Range
We observe that the domain of the exponential function is R the set of all real numbers and the range is the set \((0, \infty)\) as it attains only positive values.
Domain : R
Range : \((0, \infty)\)