Here, you will learn domain and range of greatest integer function and properties of greatest integer function with example.
Let’s begin –
Greatest Integer Function or Floor Function
For any real number x, we use the symbol [x] or \(\lfloor x \rfloor\) to denote the greatest integer less than or equal to x. For example,
[2.75] = 2, [3] =3, [0.74] = 0, [-7.45] = -8 etc.
The Function f : R \(\rightarrow\) R defined by f(x) = [x] for all x \(\in\) R is called the greatest integer function or the floor function.
It is also called a step function.
Domain and Range
Clearly. domain of the greatest integer function is the set of all real numbers and the range is the set Z of all integers as it attains only integer values.
Domain : R
Range : Z
The graph of the greatest integer function is shown in figure.
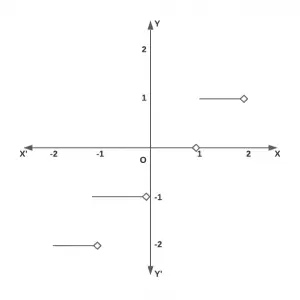
Greatest integer function
Properties of Greatest Integer Function
If n is an integer and x is a real number between n and n + 1, then
(i) [-n] = -[n]
(ii) [x + k] = [x] + k, for any integer k.
(iii) [-x] = -[x] – 1
(iv) [x] + [-x] = \(\begin{cases} -1, & \text{if}\ x \notin Z \\
0, & \text{if}\ x \in Z \end{cases}\)
(v) [x] – [-x] = \(\begin{cases} 2[x] + 1, & \text{if}\ x \notin Z \\
2[x], & \text{if}\ x \in Z \end{cases}\)
(vi) [x] \(\ge\) k \(\implies\) x > k, where k \(\in\) Z
(vii) [x] > k \(\implies\) x \(\ge\) k + 1, where k \(\in\) Z
(viii) [x] > k \(\implies\) x \(\ge\) k + 1, where k \(\in\) Z
(ix) [x] < k \(\implies\) x < k, where k \(\in\) Z
(x) [x + y] = [x] + [y + x – [x]] for all x, y \(\in\) R
Example : If y = 2[x] + 3 & y = 3[x – 2] + 5, then find [x + y] where [.] denotes greatest integer function.
Solution : y = 3[x – 2] + 5 = 3[x] – 1
so 3[x] – 1 = 2[x] + 3
[x] = 4 \(\implies\) 4 \(\le\) x < 5
then y = 11
so x + y will lie in the interval [15, 16)
so [x + y] = 15
Hope you learnt domain and range of greatest integer function, learn more concepts of function and practice more questions to get ahead in the competition. Good luck!