Area of Frustum of Cone – Formula and Derivation

Here you will learn formula for the total surface area and curved surface area of frustum of cone with derivation and examples.

Let’s begin –

What is Frustum of Cone ?

Frustum of a cone is the solid obtained after removing the upper portion of the cone by a plane parallel to its base. The lower portion is the frustum of a cone.

Height : The perpendicular distance between the aforesaid plane and the base is called the height of the frustum.

Area of a Frustum of a Cone

(i) Curved Surface Area (C.S.A) or Lateral Surface Area

C.S.A = $\pi(r_1 + r_2)l$

(ii) Total Surface Area (T.S.A)

T.S.A = $\pi(r_1 + r_2)l$ + $\pi{r_1}^2$ + $\pi{r_2}^2$

where $l$ is the slant height of the frustum, $r_1$, $r_2$ are the radii of the base and the top of frustum of a cone.

Note : Height h of the frustum is given by the relation,

$l^2$ = $h^2$ + $(r_1 – r_2)^2$

Also Read : Volume of a Frustum of a Cone – Formula and Derivation

Derivation :

Let $r_1$ and $r_2$ be the radii of the bottom and top of the frustum respectively and $l$ be the slant height of the frustum.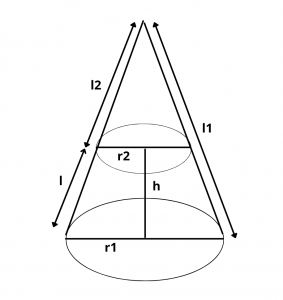

Curved Surface area of bigger cone – curved surface area of smaller cone

= $\pi r_1l_1$ – $\pi r_2l_2$

Since, [ $l_1\over r_1$ = $l_2\over r_2$ = k ]

= $\pi[r_1(kr_1) – r_2l(kr_2)]$

= $\pi k$ $[{r_1}^2 – {r_2}^2]$

C.S.A = $\pi k$$(r_1 – r_2)$$(r_1 + r_2)$ = $\pi$$(kr_1 – kr_2)$$(r_1 + r_2)$

C.S.A = $\pi$ $(l_1 – l_2)$$(r_1 + r_2)$ = $\pi l(r_1 + r_2)$

= (semiperimeter of top and bottom) $\times$ (slant height)

Total surface are of frustum = Curved surface area + area of top + area of bottom

T.S.A = $\pi(r_1 + r_2)l$ + $\pi{r_1}^2$ + $\pi{r_2}^2$

Example : A friction clutch is in the form of the frustum of a cone, the diameters of the ends being 8 cm, and 10 cm and length 8 cm. Find its bearing Surface area.

Solution : Here, radius,

$r_1$ = $10\over 2$ = 5cm,

$r_2$ = $8\over 2$ = 4cm

Slant height, l = 8 cm

Area of the bearing surface of the cone = $\pi(r_1 + r_2)l$

= 3.14(4 + 5) $\times$ 8 = 226.08 $cm^2$