Area of a Ring

Here you will learn what is the formula for the area of circular ring and examples based on it.

Let’s begin –

Let R and r be the outer and inner radii of a ring.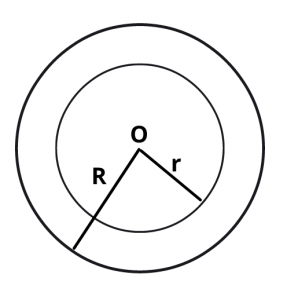

Then, area of a ring = \(\pi(R^2 – r^2)\)

We know that area of circle = \(\pi r^2\)

To calculate the area of ring (concentric circle), we subtract area of smaller circle from the area of bigger circle.

So, Area of rings = Area of bigger circle – Area of inner circle

= \(\pi R^2\) – \(\pi r^2\)

= \(\pi(R^2 – r^2)\)

Hence, the area is \(\pi(R^2 – r^2)\).

Example : Find the area of the circular ring whose outer radius is 5 cm and inner radius is 4 cm.

Solution : Here, R = 5 cm and r = 3 cm

So, Area = \(\pi(R^2 – r^2)\) = \(3.14 \times (25 -16)\) = \(3.14 \times 9\) = 28.26

Example : The area enclosed between two concentric is 770 \(cm^2\). If radius of the outer circle is 21 cm, find the radius of the inner circle.

Solution : Radius of outer circle = 21 cm

Area enclosed between two concentric circles = 770 \(cm^2\)

Let the radius of inner circle be r.

Then, according to question

\(\pi (21)^2\) – \(\pi r^2\) = 770

\(\implies\) \(21^2\) – \(r^2\) = \(770 \times 7\over 22\)

\(\implies\) \(r^2\) = 441 – \(70 \times 7\over 2\) = 441 – 245 = 196

\(\implies\) r = \(\sqrt{196}\) = 14 cm

Hence, the radius of inner circle is 14 cm.