What is Signum Function – Graph, Domain and Range

Here you will learn what is signum function definition, graph, domain and range.

Let’s begin –

What is Signum Function ?

Definition : The function f defined by

f(x) = \(\begin{cases} | x |\over x, & \text{if}\ |x| \ne 0 \\ 0, & \text{if}\ x = 0 \end{cases}\)

or,

f(x) = \(\begin{cases} 1, & \text{if}\ x > 0 \\ 0, & \text{if}\ x = 0 \\ -1, & \text{if}\ x < 0 \end{cases}\)

is called the signum function.

Also Read : Types of Functions in Maths – Domain and Range

Graph :

The graph of the signum function is shown below :

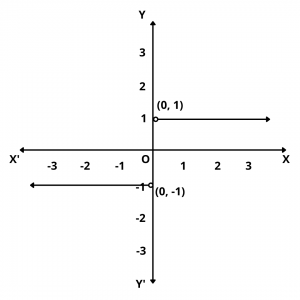
Domain and Range of Signum Function

The domain of the signum function is the set R of all real numbers and the range is the set {-1, 0, 1}.

Domain : R

Range : {-1, 0, 1}